考虑风电不确定性的含海上风电场电力系统优化调度策略研究

doi:10.16513/j.2096-2185.DE.2106547

考虑风电不确定性的含海上风电场电力系统优化调度策略研究

张晋华¹^,², 朱悦榕¹, 李旭强¹, 刘良雨¹

1．华北水利水电大学电力学院，河南省　郑州市　450045

2．新能源电力系统国家重点实验室(华北电力大学)，北京市　昌平区　102206

Optimization Scheduling Strategy of Offshore Wind Farm Power System Considering Wind Power Uncertainty

ZHANG Jinhua¹^,², ZHU Yuerong¹, LI Xuqiang¹, LIU Liangyu¹

1. School of Electric Power, North China University of Water Resources and Electric Power, Zhengzhou 450045, Henan Province, China

2. State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power University, Changping District, Beijing 102206, China

收稿日期: 2021-08-03

基金资助:

国家重点研发计划项目. 2019YFE0104800
河南省自然科学基金项目. 202300410271

Received: 2021-08-03

Fund supported:

Project supported by National Key Research and Development Program of China. 2019YFE0104800
Natural Science Foundation of Henan. 202300410271

作者简介 About authors

张晋华(1980)，女，通讯作者，博士，教授，硕士生导师，主要研究方向为风电场优化运行、风电机组功率预测；。

朱悦榕(1997)，女，硕士研究生，主要研究方向为风电场优化运行与控制；。

李旭强(1998)，男，本科生，主要研究方向为电力系统优化运行；。

刘良雨(1992)，男，硕士研究生，主要研究方向为风电场优化运行。

摘要

由于风电具有波动性和间歇性，当海上风电机组并网时，电力系统将会受到冲击，导致电网频率波动和运行控制的失调，因此需要安排其他发电机组来进行调节。在考虑海上风电机组不确定性的情况下，建立风火联合优化调度模型，以风电为主体，对电力系统优化调度策略进行研究。首先，用不同Copula函数对海上风电场功率进行拟合分析，选定t-Copula函数进行风电功率预测。在此基础上，建立了多目标的风火联合优化调度模型，将乌鸦搜索优化算法与粒子群优化算法进行收敛速度对比，选取乌鸦搜索优化算法对分析数据进行优化处理，制定全局优化调度方案。最后，算例验证了所提模型的有效性。

关键词： 风电不确定性 ; Copula函数 ; 乌鸦搜索优化算法 ; 优化调度

Abstract

Since wind power is volatile and intermittent, when offshore wind turbines are connected to the grid, the power system will be shocked, resulting in frequency fluctuations and dysregulation of the grid operation control, so other generating units need to be arranged for regulation. In this paper, considering the uncertainty of offshore wind turbines, a wind-fire joint optimal scheduling model is established to study the optimal scheduling strategy of the power system with wind power as the main body. First, different Copula functions are used to fit and analyze the offshore wind farm power, and the t-Copula function is selected for wind power prediction. On this basis, a multi-objective wind-fire joint optimal scheduling model is established, the convergence speed of the crow search optimization algorithm is compared with the particle swarm optimization algorithm, and the crow search optimization algorithm is selected to optimize the analyzed data and develop a global optimal scheduling scheme. Finally, the arithmetic example verifies the effectiveness of the proposed model.

Keywords： wind power uncertainty ; Copula function ; raven search optimization algorithm ; optimal scheduling

PDF (17025KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

张晋华, 朱悦榕, 李旭强, 刘良雨. 考虑风电不确定性的含海上风电场电力系统优化调度策略研究. 分布式能源[J], 2021, 6(5): 33-43 doi:10.16513/j.2096-2185.DE.2106547

ZHANG Jinhua, ZHU Yuerong, LI Xuqiang, LIU Liangyu. Optimization Scheduling Strategy of Offshore Wind Farm Power System Considering Wind Power Uncertainty. Distributed Energy[J], 2021, 6(5): 33-43 doi:10.16513/j.2096-2185.DE.2106547

0　引言

近年来，我国电力系统开始大规模利用可再生能源发电。海上风电场因其更高的能源容量和更自由的占用面积而引起越来越多的关注^[1]。风电的不确定性主要包括风速的波动性、间歇性及风能的随机性^[2]，这些特性使海上风电与常规能源相比供电可靠性较低，并且难以有效预测、调度和控制。考虑其不确定性的优化调度的问题被提出并得到越来越多的关注^[3]。当前风火联合优化调度的研究表明，常规火电机组的处理计划安排等对风电消纳有着非常明显的影响^[4]。消纳风电可以降低系统煤耗、减少温室气体排放量，但也会导致火电机组偏离经济运行点，甚至导致火电机组启停，从而增加火电机组单位发电煤耗。因此，从整个系统的经济性来考虑，调整火电机组的出力计划是有必要且关键的。

要对火电机组出力进行调整，首先要对海上风电场的功率进行准确预测，风电功率概率预测(又称区间预测)为此提供了一个有效的解决方案^[5]。区间预测可以为电力系统制定调度计划提供风电机组出力区间范围，以及准确的波动范围^[6]。因此，有必要在风电功率预测的基础上，进行风火联合优化调度。风电功率预测是大规模利用风电时解决风电不确定性的关键环节。与传统风电功率预测不同，风电功率概率预测得到的并不是风电功率的单点数值，而是该时刻风电功率可能出现的区间。文献[7]运用模拟退火法，产生的预测区间实际上比精确的点预测更加可靠有效。多元随机变量的分析方法也常被用于概率预测，其中Copula函数是应用最为广泛的理论。文献[8]提出了一个嵌入参数化Copula模型的深度信念网络来预测电网的小时负荷；文献[9]利用Copula函数对超短期风电预测的时间相关性进行建模，得到了预测误差的联合累积分布函数。文献[10]针对风电场出力特征，引入高维动态藤Copula理论，建立了多风电场预测出力及预测误差的联合分布模型，其拟合精度高、灵活性强，拟合过程与预测方法解耦。

海上风电场并网和大规模风电并网类似，需要安排诸多的常规机组的调峰调频，并根据各种算法来实现最经济的优化调度。传统优化算法分别有线性规划(linear programming, LP)、二次规划(quadratic programming, QP)和混合整数规划(mixed integer programming, MIP)。在求解方法改进上，一些研究已经取得新进展。由于海上风电场维护成本较高，文献[11,12]考虑平衡风力发电机组之间的疲劳负荷，在海上风电场采用无监督多代理系统(multi-agent system, MAS)的结构，提出了优化功率分配函数，仿真结果表明它能够有效传递功率指令，降低成本。与文献[12]优化目标相似，文献[13]基于分布式调度框架的改进型多代理一致性算法，提出了一种新颖的有功分配策略。不仅降低了成本，由于功率指令独立协调，还大大减少了海上风电场控制中心的计算量；文献[14]基于粒子群优化算法，提了一种海上风电场有功功率优化调度策略，并在形状规则和形状不规则的机组数量不等的海上风电场进行模拟，证明了其策略的优越性。文献[15]考虑到海上风力发电系统的成本，利用乌鸦搜索算法，解决了埃及某发电厂的经济调度和经济排放问题。

基于此，本文在考虑风力发电的不确定性的前提下及保证系统功率平衡的同时，综合海上风电机组的出力约束和火电机组出力约束及爬坡约束，并考虑系统旋转备用，最终以海上风电机组和火电机组总运行成本最小为目标函数进行构建风火联合优化调度模型。以我国某风电场2—3月风机出力数据和风速数据，采用本文所建立的模型，使用乌鸦搜索优化算法对优化模型进行求解，验证模型的有效性。

1　Copula函数分析及预测风电功率

1.1　基本原理

1.1.1　Copula函数定义

以二元为例，若H(x，y)是一个具有连续边缘分布的F(x)与G(y)的二元联合分布函数，则存在唯一的Copula函数C，使得H(x，y)＝C(F(x)，G(y))。反之，如果C是一个Copula函数，而 F和G是2个任意的概率分布函数，那么由上式定义的H函数一定是一个联合分布函数，且对应的边缘分布刚好就是F和G^[16]。任何多元联合分布都可以写成单变量边际分布函数和一个描述2个变量之间依赖结构的连接函数。换句话说，一个联合分布关于相关性的性质，完全由其Copula函数决定。如果H，F和G已知，则Copula函数可以表达为

(1) $C (u, v) = H (F^{- 1} (u), G^{- 1} (v))$

这里F^－1(u)为F(u)的反函数，也称逆累积分布函数(inverse cumulative distribution function, ICDF)。

假设x₁, x₂，…，x_N是N个随机变量，他们各自的边缘分布为F₁(x₁)，F₂(x₂)，…，F_N(x_N)，他们的联合分布为H(x₁，x₂，…，x_N)。由边缘分布的ICDF的逆变换，即x_i＝ $F_{i}^{- 1}$ (u_i)(i＝1，2，…，N)，则可以得到Copula函数的数学形式为

(2) $\begin{array}{l} C (u_{1}, u_{2}, \dots, u_{N}) \\ = H [F_{1}^{- 1} (u_{1}), F_{2}^{- 1} (u_{2}), \dots, F_{N}^{- 1} (x_{N})] \end{array}$

其作为构造二维分布族的起点，可用于多元模型分布和随机模拟，因此Copula函数被用作各种领域来求解复杂的变量关系。

1.1.2　Copula函数的种类

第一类是椭圆Copula函数族，通过已知的多元分布来计算出来的。最常见的是多元正态分布的Copula函数，即高斯Copula函数。对于一个给定的协方差矩阵，基于参数矩阵R的高斯Copula可以表达为

(3) $C_{R}^{Gauss} (u) = Φ_{R} [Φ^{- 1} (u_{1}), \dots, Φ^{- 1} (u_{d})]$

式中t-Copula函数是由正态分布变形而得。

第二类是阿基米德Copula函数族。根据不同的生成函数可以得到不同的阿基米德Copula函数，常见有Frank Copula、Clayton Copula及Gumbel Copula。其表达式中参数θ取值越大，表明相关性程度越高。

1.2　风力发电的出力特性及不确定性因素

1.2.1　风电的出力特性

风电功率和风速两者是风速作为输入，风机出力作为输出的函数关系，其表达式为

(4) $P_{w} = {\begin{array}{l} 0, & v < v_{i} \\ P_{wr} \frac{v - v_{ci}}{v_{r} - v_{ci}}, & v_{ci} < v < v_{r} \\ P_{wr}, & v_{r} < v < v_{co} \\ 0, & v > v_{co} \end{array}$

式中：v为风机所在位置的风速；v_r为风机正常运行速度(达到满发时)，一般为12 m/s；P_wr是风电机组正常发电时的功率(满发功率)；v_ci为风机开始工作(风机切入)时的风速，一般为3 m/s；v_co为风机停止工作(风机切出)时的风速，一般为25 m/s^[15]。

本文截取某海上风机组2—3月风机出力数据和实测风速数据，其中数据清洗按照风机出力函数来进行排除，其各种风速具体参数按上述标准来定。

1.2.2　风电的不确定性因素

风电的不确定性因素主要分为两方面，分别阐述如下。

风速的不确定性反映在风向、平均风速及脉动风速等要素的时空分布上，受到地形、空气密度和尾流效应等的影响。平均风速最常用的概率模型是Weibull分布，其尺度参数和形状参数由观测到的风速的期望和标准差来折算^[17]。风速的不确定性表现为波动性和间歇性两种特性。由于风速时空分布不同，对其预测的准确性往往不尽如意，风电不确定性对电力系统的影响其评估结果往往偏差很大。文献[18,19]采用了频域模型来对风电功率的波动特性进行了描述并研究了时频的快速变换。

此外，风机切入、切出过程中可能会发生故障或风速越限，导致风机非正常切入、切出，同时远程调节有可能会影响最大风电功率的追踪以及风机的出力特性变化。因此，风机工作状态转换时同样具有一定的不确定性。

1.3　基于Copula函数对风速及风功率的相关性分析

海上风电场的规划需考虑不确定性问题，传统方法大多采用Weibull分布来对风速的概率模型进行建模。预测方法有基于点预测的解析法、基于区间预测的拟合法、基于场景预测的仿真法等。

本文采取1 088组风机数据(已做数据清洗)，采用高斯Copula函数、t-Copula函数、Gumbel-Copula函数、Frank-Copula函数来对其进行分布函数建模，并计算斯皮尔曼秩相关系数来分析其相关性。通过构造各种Copula函数对数据处理后的分布函数图，来初步筛选合适的函数，计算其对原始数据的平方欧式距离，来选择更合适的Copula函数进行预测分析。

1.3.1　Copula函数分布检验

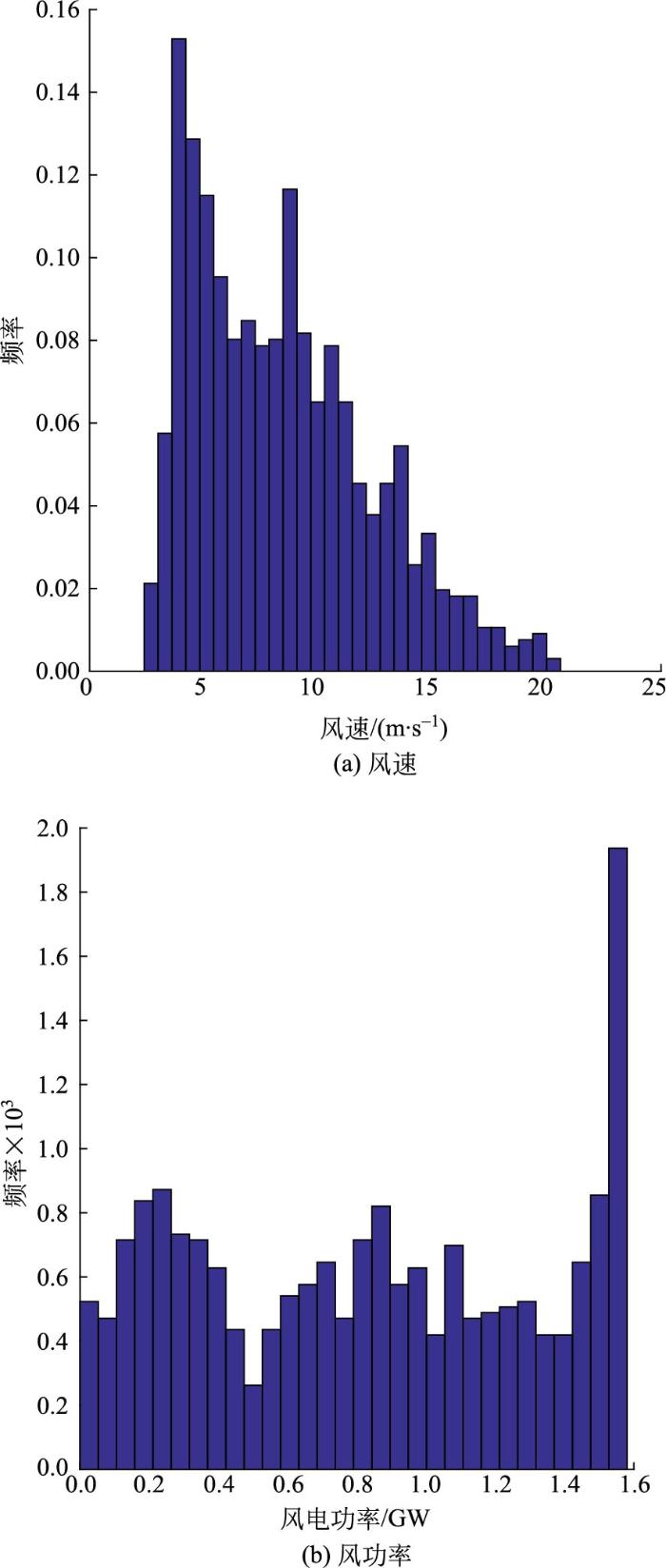
算法环境为Matlab 2018a，采取的1 088组数据为2—3月海上风机风电功率数据和实测风速数据，通过风速和风电功率数据来预测相应的风电功率区间，故不考虑风机切入或切出时的风速和风电功率数据。首先绘制频率直方图，如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 风速和风电功率的频数直方图

Fig.1 Frequency histogram of wind speed and wind power

从图1中可以看出风速的不稳定性，以及海上风电机组出力的不确定性。这样的风电并入电力系统中，将对电力系统形成强大的冲击，导致系统频率不稳定，电能质量下降，辅助服务成本提高。风机出力范围大部分分布在200～1 200 kW，较为均匀。图2为风速和风电功率的经验分布函数和核分布估计函数，蓝色为经验分布函数，黑色为核分布估计函数。同时对风速和风机出力进行正态性检验：Kolmogorov Smirnov检验(K-S检验)、Jarque-Bera检验和Lilliefors检验，得表1。

表1 风速和风电功率的检验值

Table 1 Test values of wind speed and wind power

比较项目		K-S	Jarque-Bera	Lilliefors
风速	h	1	1	1
风速	p	2.723 7×10^－6	1×10^－4	1×10^－4
风功率	h	1	1	1
风功率	p	8.857 7×10^－8	1×10^－4	1×10^－4

新窗口打开| 下载CSV

图2

新窗口打开| 下载原图ZIP| 生成PPT

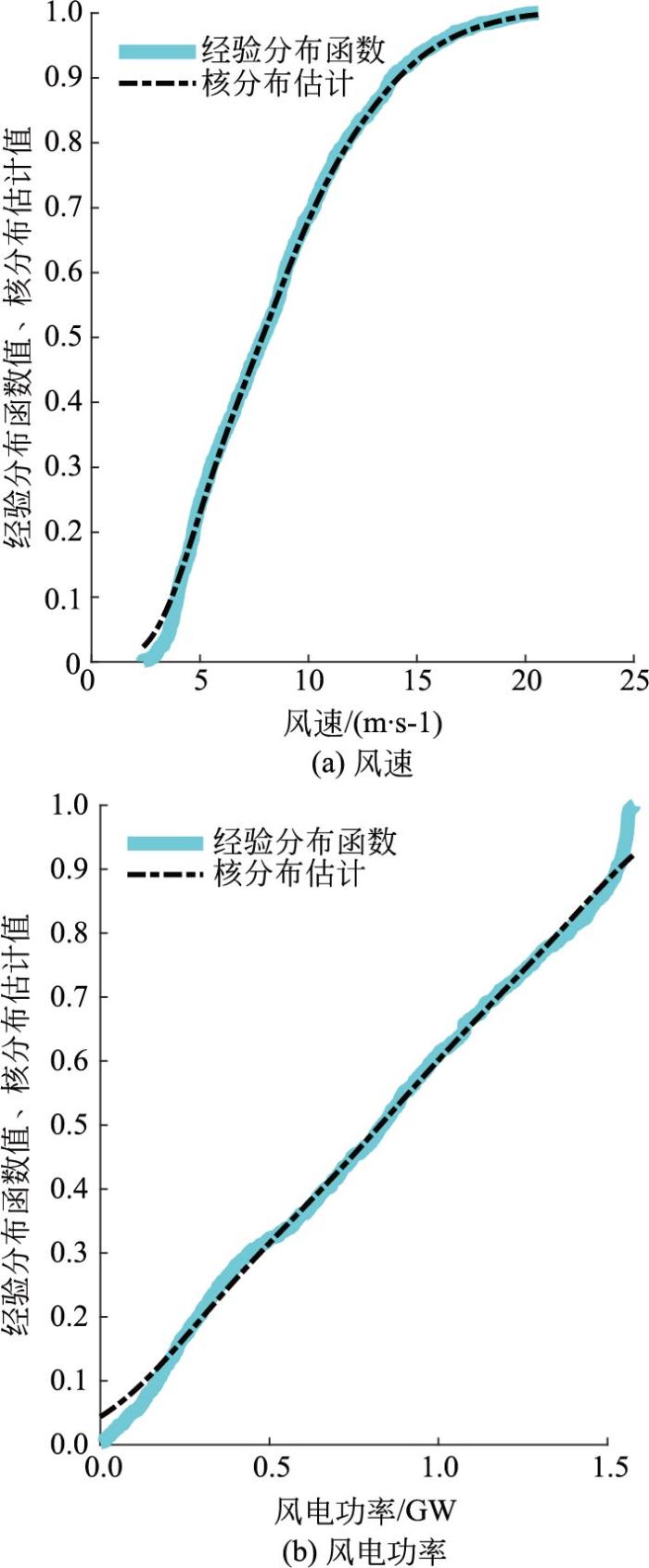
图2 风速和风电功率的经验分布函数和核分布估计图

Fig.2 Empirical distribution functions and kernel distribution estimates of wind speed and wind power

因此，风速和风电功率都近似正态分布，故认为两者符合正态分布。接下来将两者数据代入二元高斯Copula、t-Copula、Gumbel Copula和Frank Copula函数并做出两者的相应的分布函数图和密度函数图以及风电功率和风速的经验Copula分布函数图和边缘分布频数直方图，如图3，图4，图5，图6，图7，图8。

图3

新窗口打开| 下载原图ZIP| 生成PPT

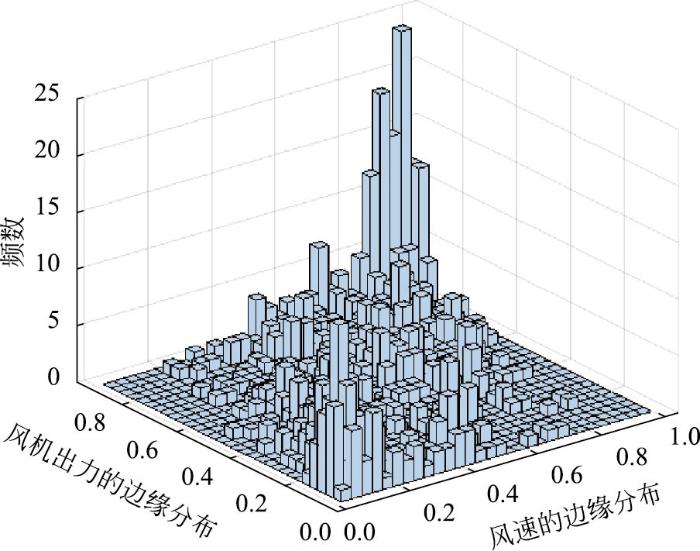
图3 风速和风机出力的边缘分布频数直方图

Fig.3 Frequency histogram of the marginal distribution of wind speed and fan output

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 经验Copula函数分布函数

Fig.4 Empirical Copula function distribution function

图5

新窗口打开| 下载原图ZIP| 生成PPT

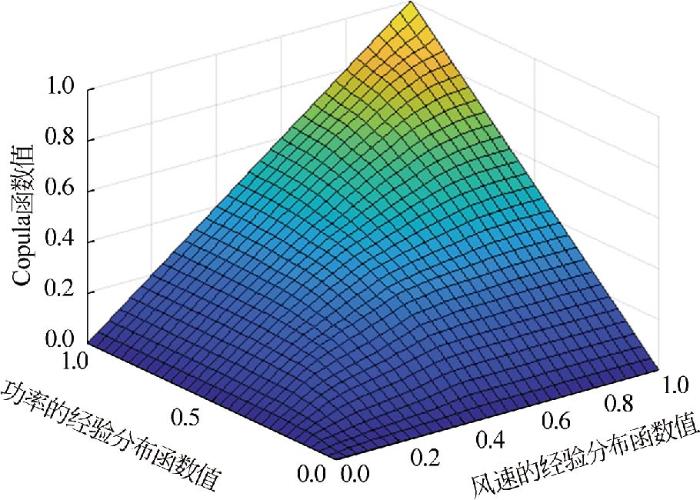
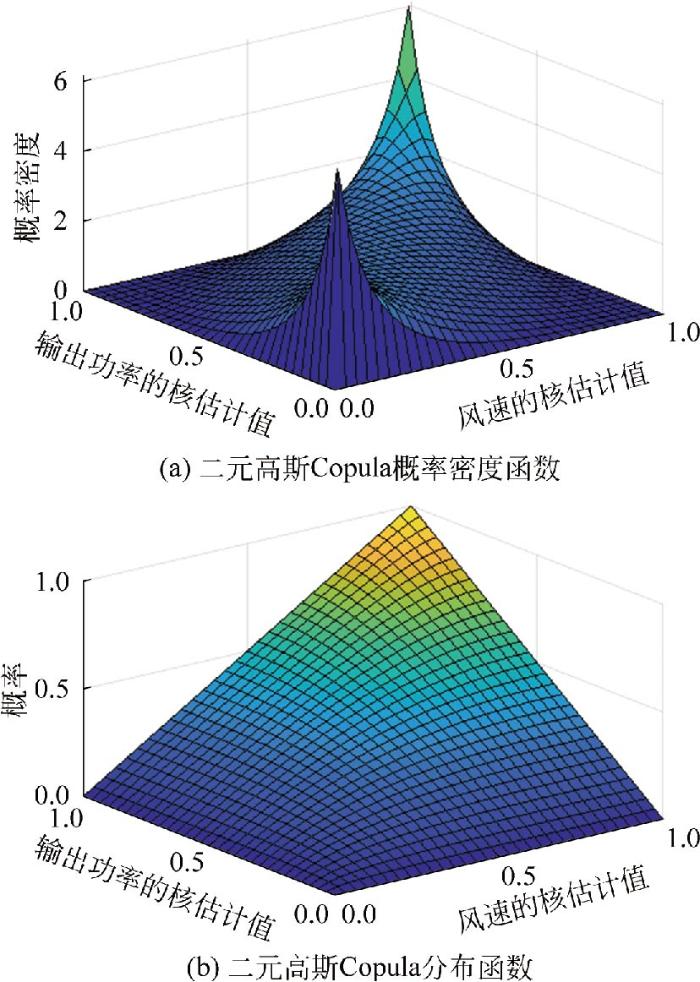
图5 二元高斯Copula的概率密度函数和分布函数

Fig.5 Probability density function and distribution function of binary Gaussian Copula

图6

新窗口打开| 下载原图ZIP| 生成PPT

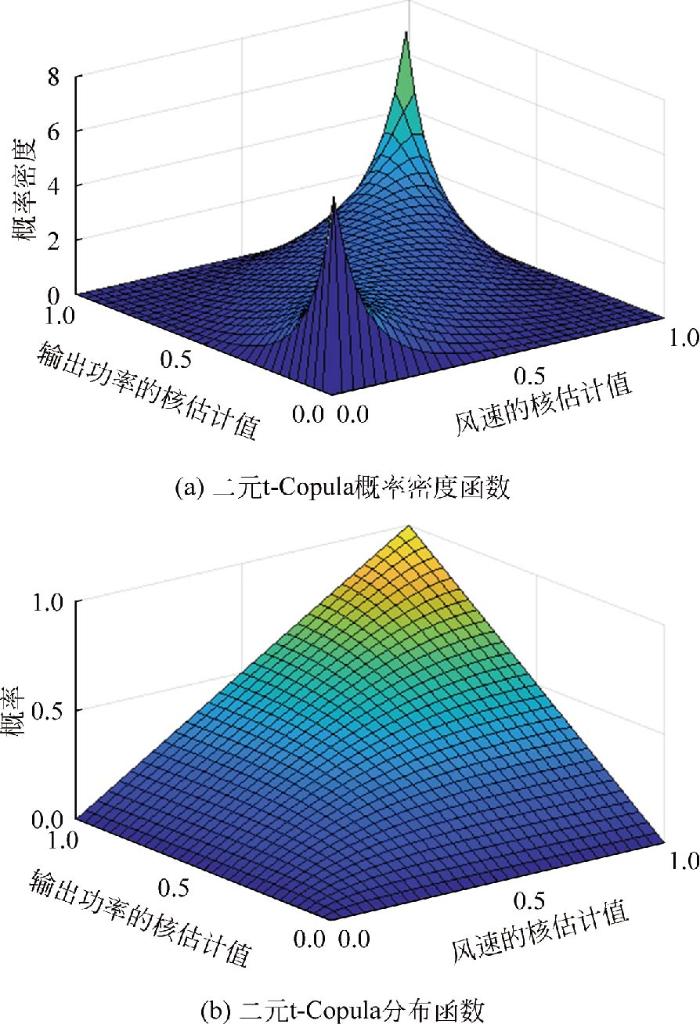
图6 二元t-Copula概率密度函数和分布函数

Fig.6 Probability density function and distribution function of binary t-Copula

图7

新窗口打开| 下载原图ZIP| 生成PPT

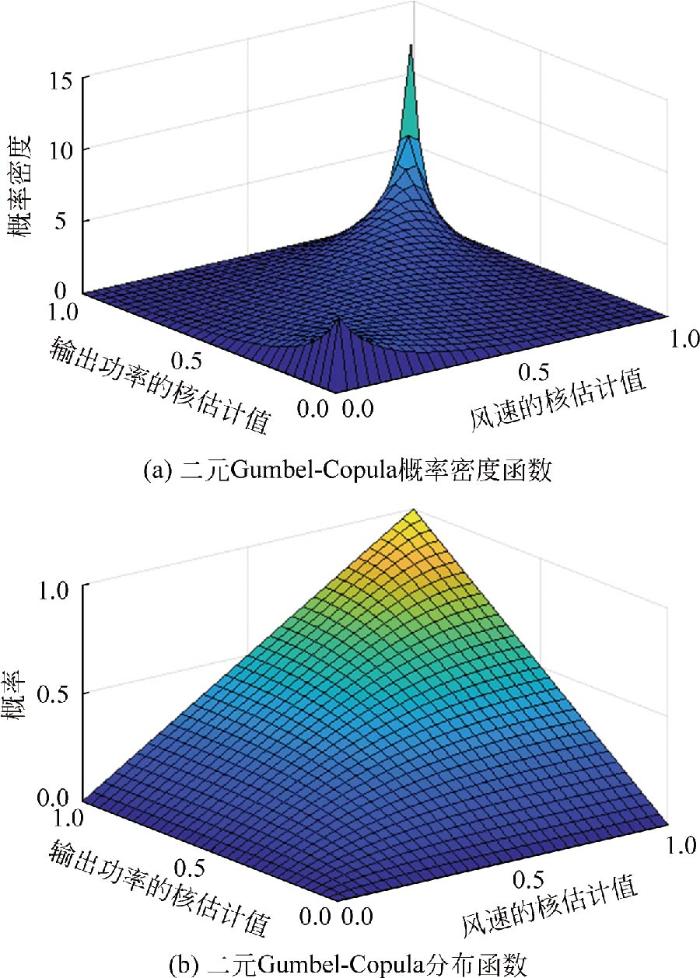
图7 二元Gumbel-Copula概率密度函数和分布函数

Fig.7 Probability density function and distribution function of binary Gumbel-Copula

图8

新窗口打开| 下载原图ZIP| 生成PPT

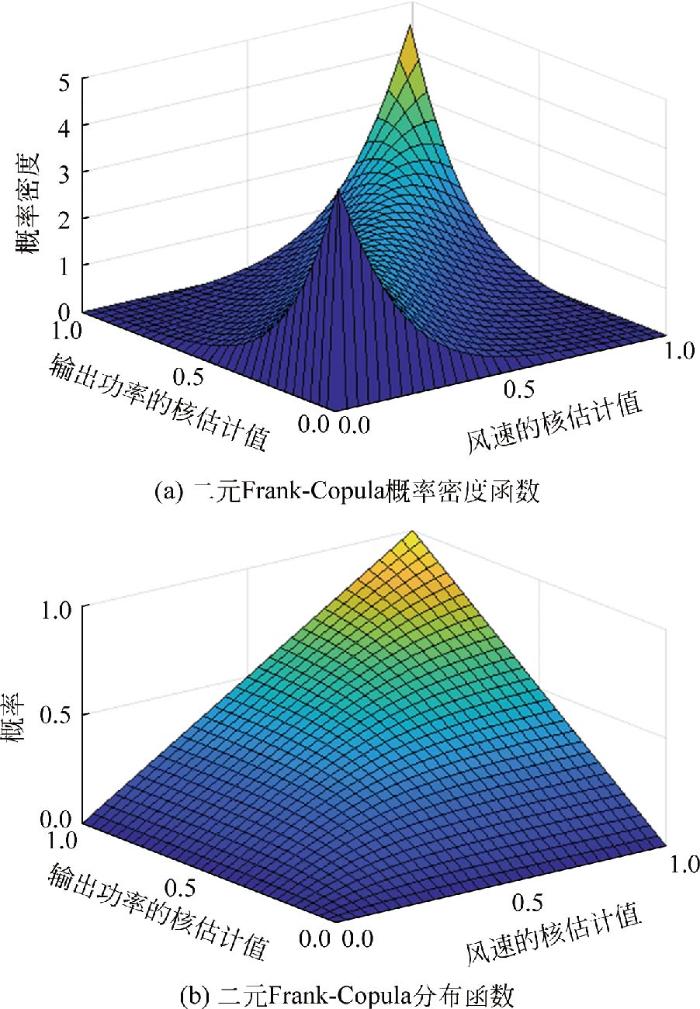
图8 二元Frank-Copula概率密度函数和分布函数

Fig.8 Probability density function and distribution function of binary Frank-Copula

图3、图4证明了二者整体呈正态分布。通过比较，二元正态Copula和t-Copula的概率函数图和分布函数图更加接近原数据的分布图。同时，本文又计算了各个Copula函数的斯皮尔曼秩相关系数和肯德尔秩相关系数，从而得出风速与风电功率的相依赖性极强且价值极高。后计算得出4种Copula函数与原始数据的平方欧式距离分别为0.850 9、0.089、0.108 5、0.058。因此，本文采用t-Copula函数来对风电功率进行区间预测。

1.3.2　风电功率的区间预测

以海上风机数据为准，设置相关参数t＝1，误差参数位0.000 1，对1 088组数据进行汇总预测得风电功率预测区间。最小出力为377.542 6 MW，最大出力为755.088 9 MW。由于风速的时空分布特点，此外还用时变Copula函数来对风电功率进行预测。

在风速正常且稳定、不考虑切入切出故障情况下，各时变Copula函数的出力预测区间如表2。

表2 时变Copula函数的预测区间

Table 2 Prediction interval of time-varying Copula function　MW

比较项目	最小出力	最大出力
Gauss Copula	385.868 1	771.741 7
Gumbel Copula	366.131 6	732.282 4
SJC Copula	345.469 5	690.977 6

新窗口打开| 下载CSV

由此，加入时间因素后，原预测区间最大最小出力波动并不明显。图9，图10，图11分别为时变高斯Copula函数、时变Gumbel Copula函数和时变SJC Copula函数对两者的依赖性分析，三者的依赖性分别为0.7左右、0.6左右和1.8～1.9，说明加入时间因素对其两者的干扰。同时，时变高斯Copula函数的预测区间更接近t-Copula函数的预测值，也更加说明两者在加入时间因素后更加符合正态分布。故此，可以基本认定采用t-Copula函数对风电功率区间预测的正确性和准确性。

图9

新窗口打开| 下载原图ZIP| 生成PPT

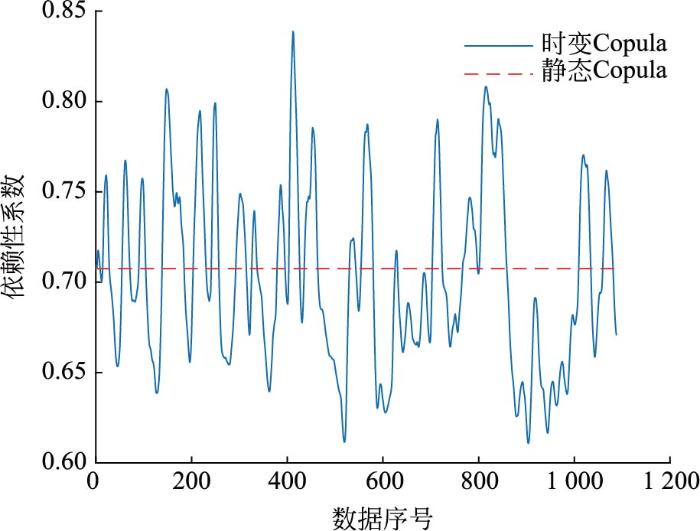
图9 时变高斯Copula函数的依赖性分析

Fig.9 Dependence analysis of time-varying Gaussian Copula functions

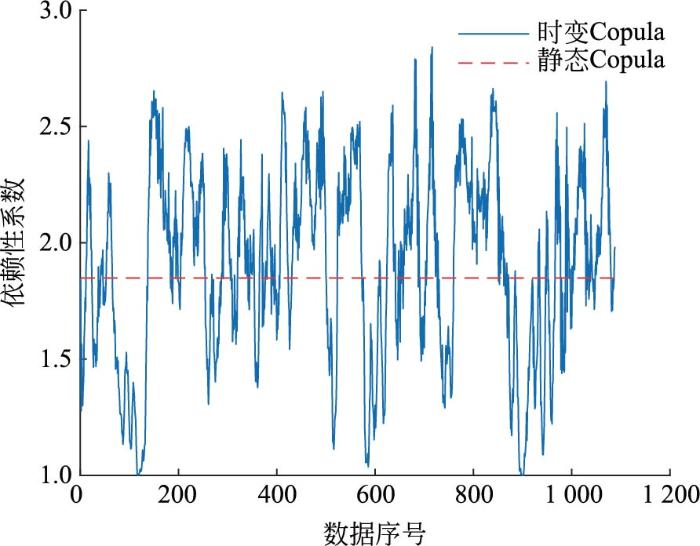
图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 时变Gumbel Copula函数的依赖性分析

Fig.10 Dependence analysis of time-varying Gumbel Copula functions

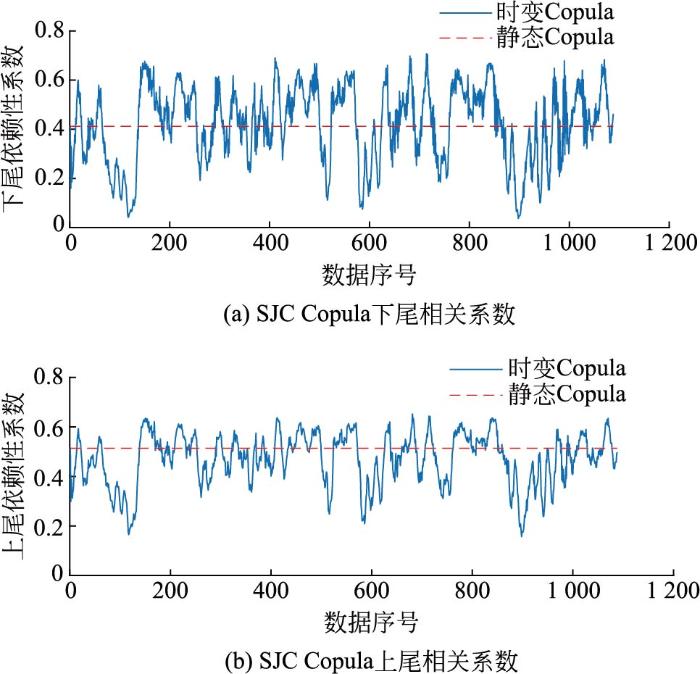
图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 时变SJC Copula函数的依赖性分析

Fig.11 Dependence analysis of time-varying SJC Copula functions

2　风火联合优化调度建模

2.1　风火优化调度模型的建立

2.1.1　目标函数

目标函数的构造主要分为火电机组的燃煤消耗和启停成本C₁、海上风电机组的出力成本C₂、系统旋转备用成本C₃与环境保护税收C₄，表达式为

(5) $F = min (C_{1} + C_{2} + C_{3} + C_{4})$

在火电机组调度给风电调峰服务时，其运行成本主要包括燃煤消耗和启停成本，如式(6)(7)。风电的运行成本函数如式(8)。考虑到预测风电功率的误差，系统需要在原基础上额外提供一定的旋转备用。火电机组提供的旋转备用成本函数如式(9)。由于环境保护，消耗燃煤将产生SO₂和NO_x造成污染，将需要缴纳一定的环境保护税，这部分成本如式(10)(11)。

(6) $\begin{array}{l} C_{1} (P_{g} (i, t)) = & \sum_{t = 1}^{T} \sum_{i = 1}^{N_{g}} [u_{g} (i, t) f (P_{g} (i, t)) + \\ u_{g} (i, t) (1 - u_{g} (i, t - 1)) S_{g} (i)] \end{array}$

(7) $f (P_{g} (i, t)) = (a P_{g}^{2} (i, t) + b P_{g} (i, t) + c) P_{coal}$

(8) $C_{2} = \overset{T}{\sum_{t = 1}} ρ_{w} P_{w} (t)$

(9) $C_{3} = \overset{T}{\sum_{t = 1}} ρ_{res} e_{w} P_{w} (t)$

(10) ${\begin{array}{l} H_{S} = C_{1} q_{S} (1 - η_{S}) / P_{coal} \\ H_{N} = C_{1} q_{N} (1 - η_{N}) / P_{coal} \end{array}$

(11) $C_{4} = K [(H_{S} / J_{S}) + (H_{N} / J_{N})]$

式中：P_g(i，t)为第t时段火电i号机组的出力；N_g为火电机组的总台数；T为一个优化调度周期的时间，本文设置为24 h，1h为一个时段；u_g(i，t)是第t时段的第i号机组的启停状态，u_g(i，t)＝1表示机组处于启动状态，u_g(i，t)＝0表示机组处于停机状态；S_g(i)表示火电第i号机组启停成本，这里将启停成本统一折算到启动成本中；f(P_g(i，t))为火电机组的运行燃料消耗函数；P_coal为燃煤单价；a、b、c为函数的对应机组的常系数；ρ_w为风电运行成本系数；P_w(t)为t时刻的风电出力；ρ_res为系统旋转备用成本系数；e_w为风电预测误差率系数；q_S、q_N分别为单位质量煤炭燃烧生成的SO₂和NO_x的质量；η_S、η_N分别为燃煤环节的环保装置脱除SO₂和NO_x的效率；J_S、J_N分别为SO₂和NO_x的污染当量数；K为每单位污染当量数所需要缴纳的环境保护税。

2.1.2　约束条件

风火联合运行时要考虑自身的一些约束及电力系统正常运行的约束，包含系统功率平衡约束、系统正负旋转备用约束、海上风电机组出力约束、火电机组出力约束、火电机组爬坡约束以及火电机组启停时间约束，分别如式(12)—(17)。

(12) $\overset{N_{g}}{\sum_{i = 1}} P_{g} (i, t) + P_{w} (t) = P_{D} (t)$

(13) ${\begin{array}{l} \sum_{i = 1}^{N_{g}} [P_{g-max} (i) - P_{g} (i, t)] \geq μ_{d 1} P_{D} (t) + μ_{w 1} P_{w} (t) \\ \sum_{i = 1}^{N_{g}} [P_{g} (i, t) - P_{g-min} (i)] \geq μ_{d 2} P_{D} (t) + μ_{w 2} P_{w} (t) \end{array}$

(14) $0 \leq P_{w} (t) \leq P_{w-max}$

(15) $u_{g} (i, t) P_{g-min} (i) \leq P_{g} (i, t) \leq u_{g} (i, t) P_{g-max} (i)$

(16) ${\begin{array}{l} u_{g} (i, t) P_{g} (i, t) - u_{g} (i, t - 1) P_{g} (i, t - 1) \leq \\ r_{g-up} (i) \\ u_{g} (i, t - 1) P_{g} (i, t - 1) - u_{g} (i, t) P_{g} (i, t) \leq \\ r_{g-down} (i) \end{array}$

(17) ${\begin{array}{l} \sum_{k = t}^{t + T_{on} - 1} u_{g} (i, k) \geq T_{on} [u_{g} (i, t) - u_{g} (i, t - 1)] \\ \sum_{k = t}^{t + T_{off} - 1} [1 - u_{g} (i, k)] \geq T_{off} [u_{g} (i, t - 1) - u_{g} (i, t)] \end{array}$

式中：P_D(t)为预测日负荷的预测量；P_g-max(i)为第i号火电机组的最大出力；P_g-min(i)为第i号火电机组的最小出力；μ_d1、μ_d2和μ_w1、μ_w2分别为对于预测负荷误差和对于风电预测误差的正、负旋转备用约束系数；P_w-max为风电机组最大出力；r_g-up(i)、r_g-down(i)分别为第i号火电机组的爬坡速率上、下限；T_on、T_off分别为第i号火电机组最大持续开机时间和最大持续关停时间。

2.2　算法对比

粒子群优化算法是通过模拟鸟群觅食行为而发展起来的一种寻找最优值的算法。粒子群中的所有粒子根据自己的当前个体极值和整个粒子群共享的当前全局最优解来调整自己的速度和位置，循环往复，最终找到约束条件下的最优解^[8]。其流程如图12所示。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 粒子群优化算法简要流程图

Fig.12 Brief flow of particle swarm optimization algorithm

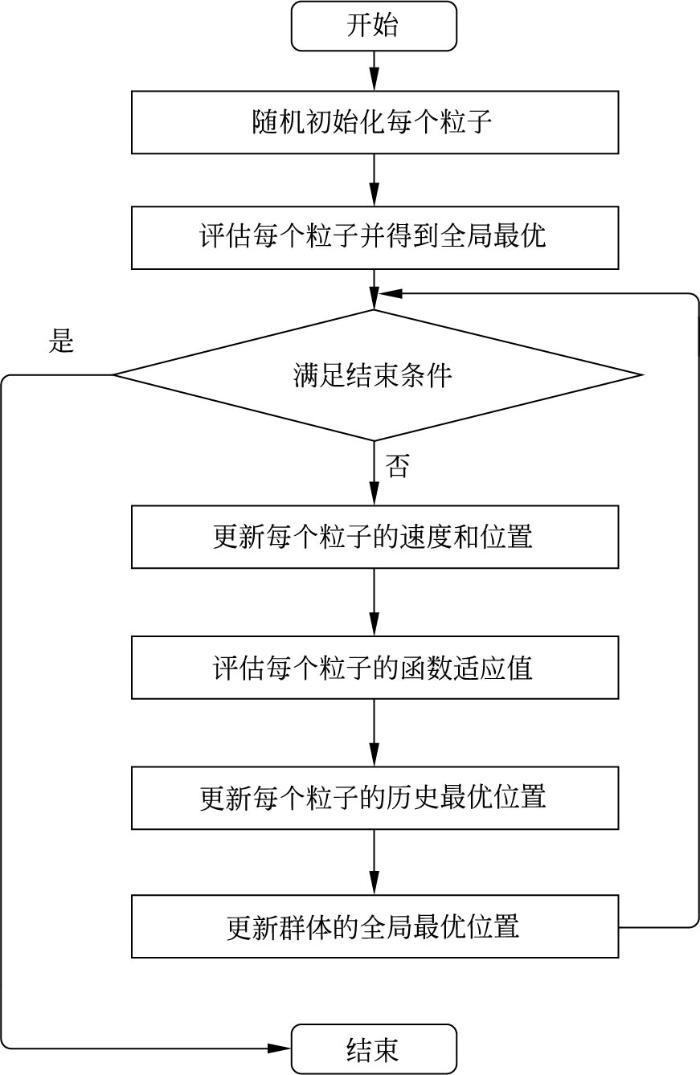
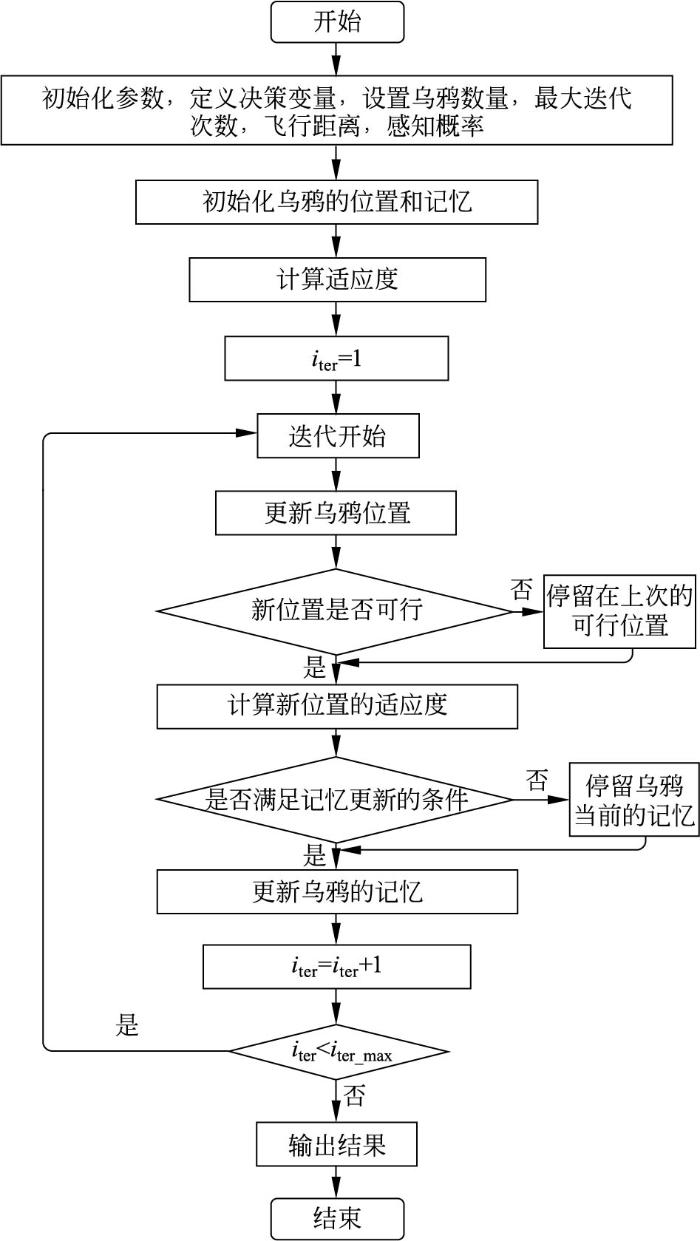
乌鸦搜索优化算法是2016年提出的群智能仿生优化算法，通过模仿乌鸦藏食这一行为来解决优化问题，其流程如图13所示。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 乌鸦搜索优化算法流程图

Fig.13 Crow search algorithm flow

粒子群优化算法中，粒子群规模为200，自变量个数为2，每个粒子的个体学习因子为c_{_1}＝1，每个粒子的社会学习因子为c_{_2}＝1，惯性因子初始值为w＝0.6，粒子的最大飞翔速度为v_max＝5，粒子飞翔速度v处于[0，2]内。乌鸦搜索优化算法中，乌鸦种群数量为200，问题维度(决策变量的数量)为2，意识概率A_P＝0.1，飞行长度f_l＝2。在Matlab 2018a软件上进行算法编译。

两种算法中的参数均为其优化算法中的一般标准，这里统一规定最大迭代次数i_{ter_max}＝300，目标函数相同，定为二元的二次函数且取其最小值(函数系数均为正)，收敛截止目标精度统一定为1。以此来对两种算法进行收敛速度对比，选择收敛速度较快的优化算法。两种算法的收敛速度如图14，图15所示。其中，横轴为迭代次数，竖轴为目标函数值。

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 粒子群优化算法收敛速度

Fig.14 Particle swarm optimization algorithm convergence speed

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 乌鸦搜索优化算法收敛速度

Fig.15 Crow search algorithm convergence speed

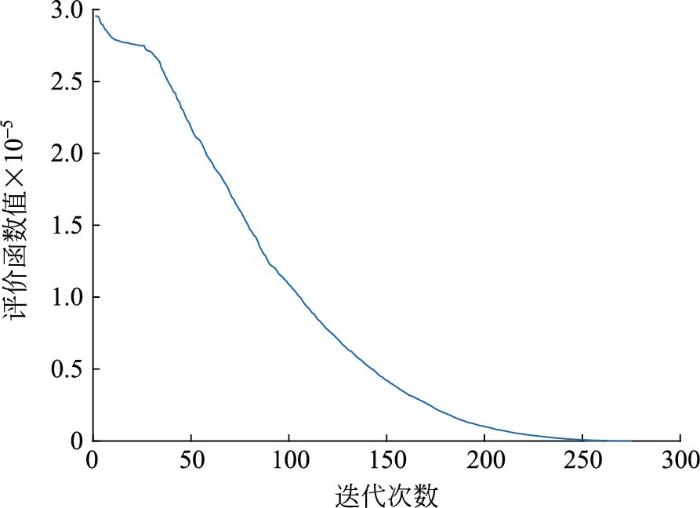
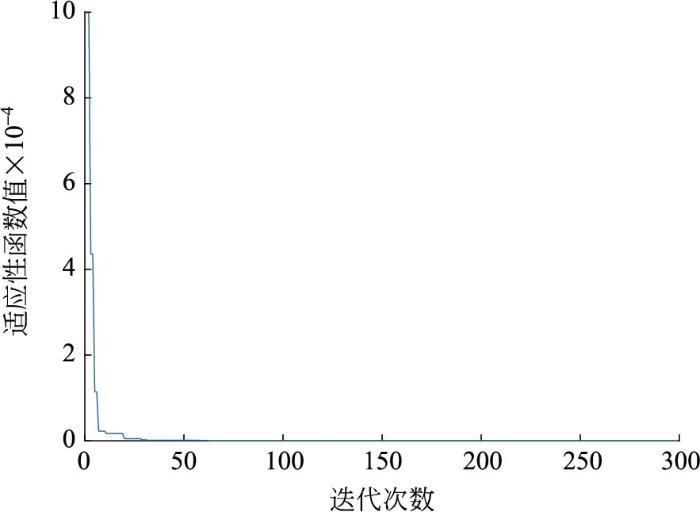
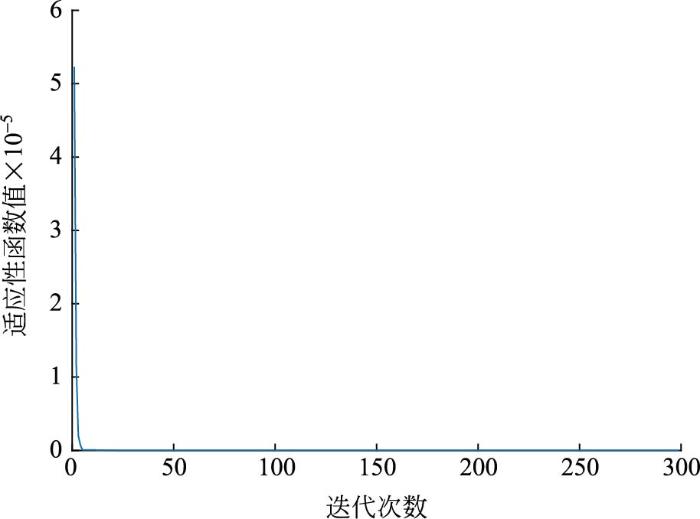
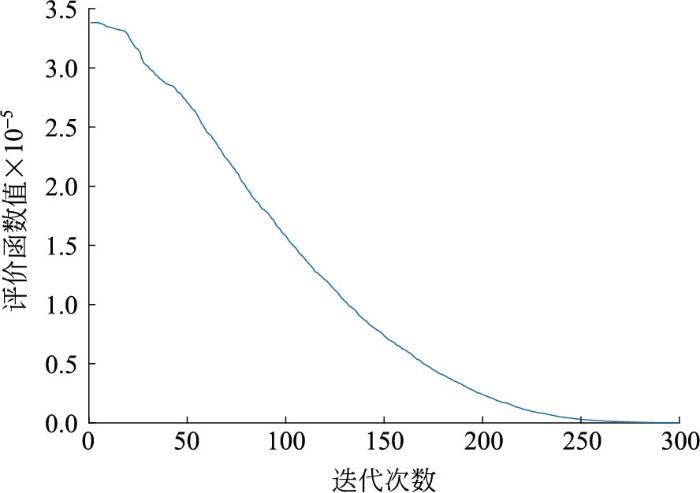
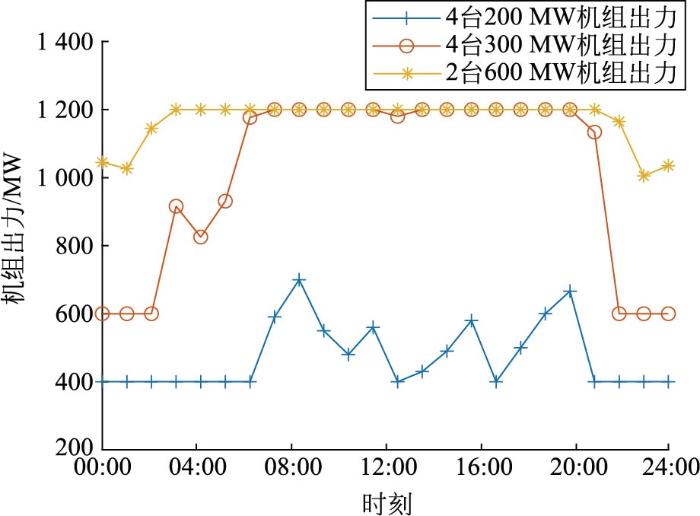
粒子群优化算法在迭代第140次时达到目标精度，乌鸦搜索优化算法在迭代第50次时达到目标精度，且乌鸦搜索优化算法其初始目标函数值远小于粒子群优化算法的初始目标函数值，收敛速度也远超粒子群优化算法。因此，选择乌鸦搜索优化算法来进行整个风火优化调度模型的最优求解。考虑各机组出力情况及其它环境或经济因素，得到全局优化调度方案，如图16。

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16 全局优化调度方案示意图

Fig.16 Schematic diagram of global optimal scheduling scheme

3　算例分析

3.1　算例说明

为验证乌鸦搜索优化算法和选择的t-Copula函数的准确性及本文所提出风火联合调度模型对短期日负荷的调度能力，本文选用文献[20]和文献[21]中的相关风电机组、火电机组和系统参数，进行算例分析。

3.2　算例结果分析

图17、图18分别为该算例下的乌鸦搜索优化算法和粒子群优化算法的收敛速度图。可以看出，乌鸦搜索优化算法在50次左右已经开始收敛，粒子群优化算法在300次左右才开始收敛，明显得出该算例下，乌鸦搜索优化算法同样具有优良的收敛速度。

图17

新窗口打开| 下载原图ZIP| 生成PPT

图17 乌鸦搜索优化算法收敛速度的仿真结果

Fig.17 Simulation results of convergence speed of crow search optimization algorithm

图18

新窗口打开| 下载原图ZIP| 生成PPT

图18 粒子群优化算法收敛速度的仿真结果

Fig.18 Simulation results of convergence speed of particle swarm optimization algorithm

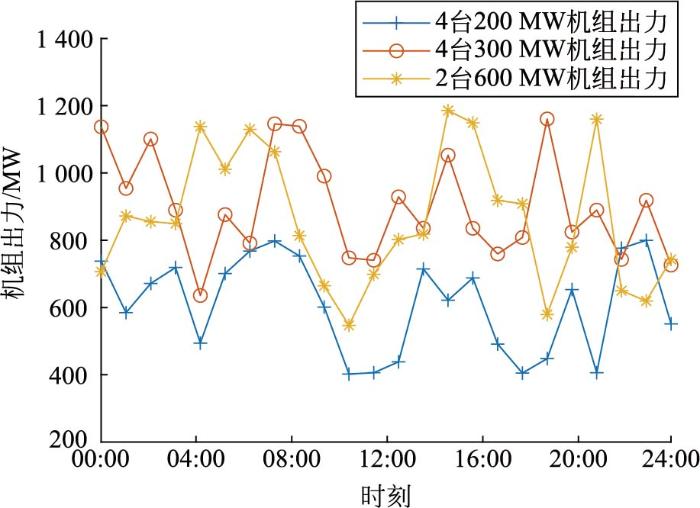
图19、图20分别为3种火电机组模拟出力情况和经优化后的3种火电机组出力情况。根据各机组优化前后的出力数据图可以看出，优化过后各机组出力平稳，进行上下爬坡时能够在约束下平滑过渡。同时，原模拟出力时，3种机组爬坡次数均有多次，优化后，多次进行爬坡的机组改为容量较小的机组进行，使实际操作更加方便，并保护了发电机组的寿命，使之能够更好更长时间使用。

图19

新窗口打开| 下载原图ZIP| 生成PPT

图19 优化前各机组模拟出力情况

Fig.19 Simulated hourly output of each unit before optimization

图20

新窗口打开| 下载原图ZIP| 生成PPT

图20 优化后各机组出力情况

Fig.20 Simulated hourly output of each unit after optimization

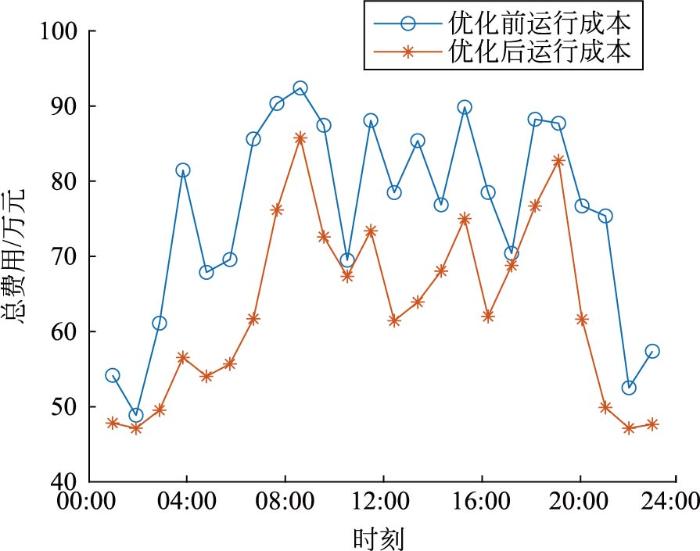
图21为优化前后的总成本对比。经过优化，运行成本明显降低，说明本文选取的Copula函数符合预期标准，证明该优化算法效益显著，本文建立的模型对预测日负荷的调度能力良好，证明了模型的正确性和算法的优良特性。

图21

新窗口打开| 下载原图ZIP| 生成PPT

图21 优化前后的总成本效益对比

Fig.21 Total cost-benefit comparison before and after optimization

4　结论

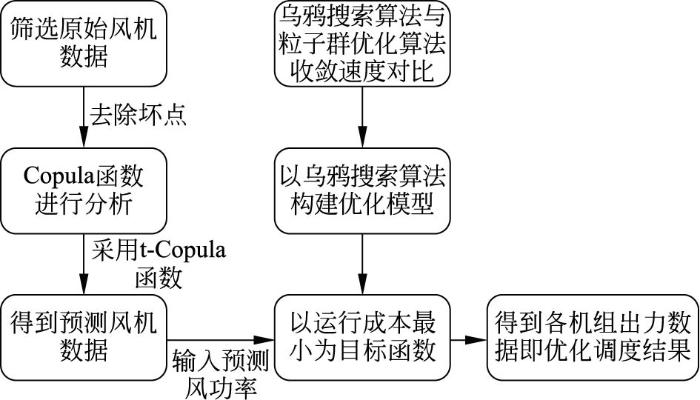
本文进行了考虑风电不确定性的含海上风电机组电力系统优化调度策略分析研究，采用效果更佳的Copula函数对风电功率进行预测，建立了风火联合优化调度模型，将乌鸦搜索优化算法与粒子群优化算法进行对比，取收敛速度较快的乌鸦搜索优化算法对数据进行迭代处理，得到各机组出力数据来进行优化调度。研究过程中得到如下结论：

1) Copula函数对相依赖性测度的分析十分明显。且作为构造二维分布族的起点，它可用于多元模型分布和随机模拟。这恰恰贴合了风电的不确定性因素，在对风电各种不确定性因素进行随机模拟中具有较高的准确度。

2)在风火联合优化调度模型中，充分考虑火电机组的相关约束，并保留了一定的备用容量来作为预测日负荷和预测风电的误差。这可作为安全稳定进行调度工作的一道保障。

3)与粒子群优化算法相比，乌鸦搜索优化算法不仅收敛速度更快，其在全局寻优方面更优于粒子群优化算法。随着飞行步长和意识概率两个参数的调整，其全局寻优能力得到有效提高。

本文在一定的时间和有限的水平下虽然做出了一定的算法及分析，但内容仍有不足，还需更加完善补充。在风电不确定性因素方面，本文仅进行了对风速和风电功率两者的分布检验和风电功率区间的预测，并没有全面考虑风机扇叶和地形因素，以及湍流效应和灯塔效应等。对于风电机组，本文仅考虑了出力约束，缺乏对其弃风率和海上风电场本身的消纳储能等因素的详细探讨。在优化算法方面，本文对于所选取的乌鸦搜索优化算法没有考虑意识概率这一因素随迭代次数的改变，故代码仍有进一步完善的空间。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

PENG

, HU

, SOLTANI

, et al.

Offshore wind farm layout design considering optimized power dispatch strategy

[J]. IEEE Transactions on Sustainable Energy, 2017, 8(2): 638-647.